How Did Eratosthenes Estimate The Size Of Earth In 240 B.c

Astronomy 101 Specials: Eratosthenes and the Size of the World

Eratosthenes' method for determining the size of the Earth was an elegant application of uncomplicated geometry to an otherwise very difficult problem. By using the divergence in the elevation of the noontime lord's day at 2 unlike locations, he was able to measure the angular deviation betwen the vertical directions at those two locations. This angular difference told him what fraction of the way around the earth separated the two locations. He and then used this fraction and the measured distance between the two locations to guess the distance around the earth (a.k.a. the circumference).

As the story goes, old Eratosthenes learned that at noon on i solar day a twelvemonth (the summer solstice, but that's not actually important), the Lord's day shone directly down a deep vertical well in a town chosen Syene, nearly 500 miles south of his home in Alexandria. Eratosthenes reasoned that the Sun must exist direct overhead at noon in Syene at this time. He knew that the Sunday was non directly overhead in Alexandria on this day, so he figured that the vertical direction in Alexandria was dissimilar from the vertical direction in Syene.

This conclusion was based on the assumption that the Sun was far enough away (compared to the altitude between Syene and Alexandria) that the rays of incoming sunlight at both locations were parallel.

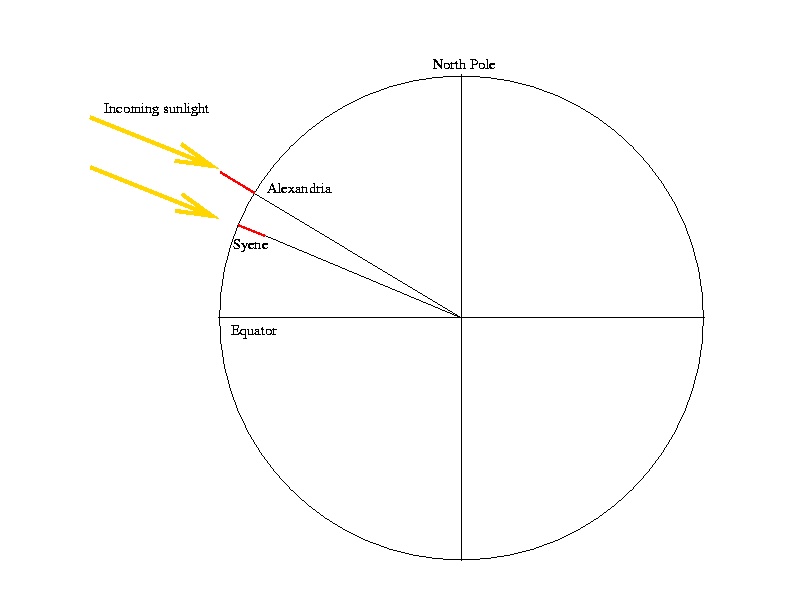
Then how unlike were the vertical directions at the two locations? Well, he decided to measure this with a vertical stick in the basis called a gnomon. He watched the shadow of the gnomon on the day in question, and measured the length of the shadow at apex. The elevation of the stick and the length of the shadow immune him to calculate the angle between the vertical at Alexandria (equally indicated by the gnomon) and the direction of the Sun's rays at noon.

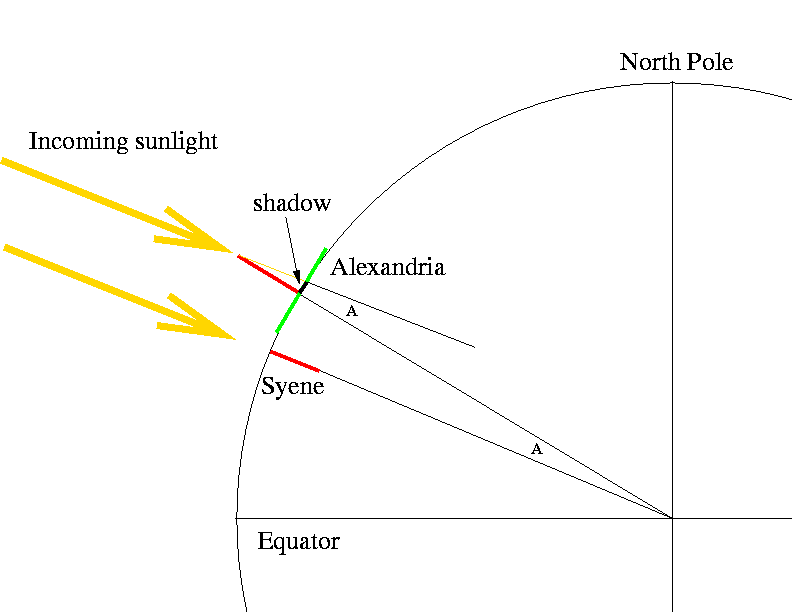
This angle, labeled ``A'' in the above cartoon, is calculated every bit follows:

tan(A) = (length of shadow)/(height of gnomon)

where tan(A) is the tangent part, which was well-known at the time. By calculating this bending, Eratosthenes had calculated the athwart departure betwixt the verticals at Syene and Alexandria. Why? Because the sunward management is the vertical management at Syene on this day. You tin can encounter this graphically in the effigy above, past noting that the sunward directions (yellow lines) are parallel, and therefore that the ii angles labeled ``A'' really accept the aforementioned value. (Recollect? A line crossing two parallel lines makes the aforementioned angle with each line?)

So Eratosthenes fabricated this measurement and found that the value for angle ``A'' is 7.2 degrees. He also knew that the actual distance betwixt Alexandria and Syene was 5040 stades (i stade = about 160 m) considering somebody had measured it out by foot. Well 7.2 degrees is only 7.2/360ths of the mode around the globe (since all the way around is 360 degrees). If that distance is 5040 stades, then the total distance around the earth must exist